电设过初赛了好开森呐～
光棍节一个人过 男生节一个人过 qaq 微积分考的再高又有卵用？
微积分
构造之美
虽然这玩意儿跟考试没啥关系，但我觉得蛮有趣的。
From. 习题课_20161030
Prob. 设$\exists f^{\prime\prime}(x),\ f(1)=6,\ f^\prime (1)=0,\ \forall x\ge 1,\ x^2f^{\prime\prime}(x)-3xf^\prime (x)-5f(x)\ge 0.$
证明：$\forall x\ge 1,\ f(x)\ge x^5+\frac{5}{x}$
考虑函数 $$g(x)=\frac{f(x)}{x^5}-(1+\frac{5}{x^6})$$ $$g^\prime(x)=\frac{x^2f^\prime(x)-5xf(x)+30}{x^7}$$
考察分子$$h(x)=x^2f^\prime(x)-5xf(x)+30$$
$$h^\prime (x)=\ x^2f^{\prime\prime}(x)-3xf^\prime (x)-5f(x)\ge 0$$
$$\therefore h(x)\ge h(1)>0 \Rightarrow g^\prime(x)>0$$
$$\therefore g(x)\ge g(1)=0$$
From. 练习题_20161106_Taylor的应用
$f(x)\in C[a,b],\ f(x)\in D^2(a,b),\ $证明$\exists \xi\in (a,b),\ s.t. $ $$\frac{\frac{f(x)-f(a)}{x-a}-\frac{f(b)-f(a)}{b-a}}{x-b}=\frac{1}{2}f^{\prime\prime}(\xi)$$
构造函数$$F(t)=\begin{vmatrix}f(t)&1&t&t^2\\f(x)&1&x&x^2\\f(a)&1&a&a^2\\f(b)&1&b&b^2\end{vmatrix}$$
$$\therefore F(x)=F(a)=F(b)=0\wedge F^{\prime\prime}(t)=\begin{vmatrix}f^{\prime\prime}(t)&0&0&2\\f(x)&1&x&x^2\\f(a)&1&a&a^2\\f(b)&1&b&b^2\end{vmatrix}$$
$$\therefore F(x)=F(a)=F(b)=0\Rightarrow F^\prime(\xi_1)=F^\prime(\xi_2)=0\Rightarrow F^{\prime\prime}(\xi)=0$$
将$F^{\prime\prime}(\xi)=0$展开即可得到答案。
听说有人期中考最后一题没做出来？
题目：$f(0)=0,\ f(1)=1,\ f^\prime (x)>0,\ $
证明 $\forall n\in \mathbb{N}^+,\ \exists \xi_{1..n}\in (0,1),\ \xi_i\neq \xi_j,\ s.t. \sum_{i=1}^n \frac{1}{f^\prime(\xi_i)}=n$
一个很自然的想法是，考虑区间 $(0,\frac{1}{n}),\ (\frac{1}{n},\frac{2}{n}),\cdots ,\ (\frac{n-1}{n},1)$，在每个区间上用一次中值定理，则有
$$f^\prime(\xi_k)=\frac{f(\frac{k}{n})-f(\frac{k-1}{n})}{\frac{k}{n}-\frac{k-1}{n}}=n(f(\frac{k}{n})-f(\frac{k-1}{n}))$$
求和即有 $\sum_{i=1}^n f^\prime(\xi_i)=n(f(1)-f(0))=n$
但是，答案里面要证导数的倒数和为0，怎么办呢？考虑反函数就好了。就酱。
听说某个智障用积分来做夹逼的题目？
错在哪里呢？夹逼得出来的答案 1 肯定没问题。
$$\lim_{n\to \infty}n\sum_{i=1}^n \frac{1}{n^2+i\pi}=1$$
然而变个形式，就是求 $$\sum_{i=1}^n \frac{1}{n+\frac{i}{n}\pi}$$
当 $n\to \infty$ 的时候，$\frac{i}{n}$ 取遍 $[0,1]$，于是把求和换成积分变成
$$\lim_{n\to\infty}\int_0^1 \frac{1}{n+x\pi}\, dx$$
就是$$\lim_{n\to\infty} \left.\frac{\ln (n+x\pi)}{\pi}\right|_{x=1}-\left.\frac{\ln (n+x\pi)}{\pi}\right|_{x=0}$$
然而 $$\lim_{n\to\infty} \frac{1}{\pi}\ln\frac{n+\pi}{n}=0$$
$\therefore 1=0\ ???$ hhh 真的了解 dx 吗
程设
为了公众号吸粉学委也是不择手段了…
大家刚考完C语言，然后这里简单讲评一下AB卷。
清华大学《计算机语言与程序设计》2016年秋季学期 期中测试 （A卷）
A1、单词替换（30分）
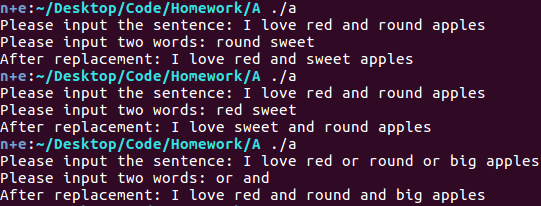
假设一个英文语句sentence，该语句中的单词是以空格为间隔的。然后有两个单词word1和word2，请将英文句子sentence中的所有单词word1用word2进行替换。
如，输入的语句为”I love red and round apples”，输入的单词分别为”round”和”sweet”，则替换后的语句为”I love red and sweet apples”。
可能有的人会把这种题写复杂了吧……这种题目不要在原串上进行操作，重新开一个串来储存结果，会好写很多。
sublime并不支持中文所以我就懒得打了。
#include <cstdio>
#include <cstring>
bool check(char *s, char *w)
{//判断两个字符串是否相等，以w为标准
for (; *w && *s; s++, w++)
if (*s != *w)
return 0;
return 1;
}
int main(int argc, char const *argv[])
{
char s[256] = "", w1[20] = "", w2[20] = "", ans[300] = "";
printf("Please input the sentence: ");
gets(s);
printf("Please input two words: ");
scanf("%s%s", w1, w2);
int l1 = 0;
for (; w1[l1]; l1++);
printf("After replacement: ");
for (int i = 0, j = 0; s[i]; i++)
if (check(&s[i], &w1[0]))
{//如果相等直接替换
for (int k = 0; w2[k]; ans[j++] = w2[k++]);
i += l1 - 1;
}
else ans[j++] = s[i];
puts(ans);
return 0;
}
/*
I love red and round apples
red sweet
*/
A2、矩阵处理（30分）
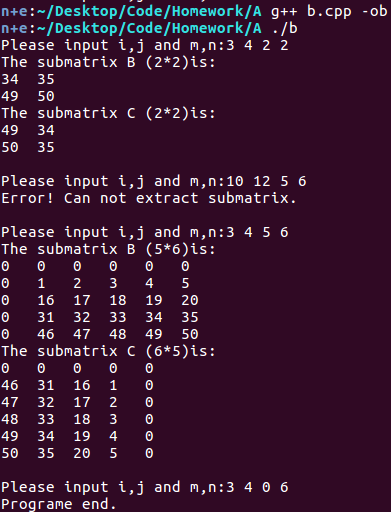
已知一个$M$行$N$列的整数矩阵$A$，请从这个原始矩阵中以$a_{i,j}$为右下角元素抽取一个$m\times n$的子矩阵$B$，要求$a_{i,j}$必须位于$A$中，如果抽取的子矩阵$B$的范围超出原始矩阵$A$的范围，则子矩阵$B$中的这些元素将赋值为$0$。最后请将子矩阵$B$顺时针旋转$90^\circ$，得到结果矩阵$C$。
如：原始矩阵$A$为$\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}$，若输入的右下角元素为$a_{1,1}$，输入的$m$、$n$分别为$2$、$3$，则子矩阵$B$为$\begin{vmatrix}0&1&2\\0&4&5\end{vmatrix}$，旋转后的结果矩阵$C$为$\begin{vmatrix}0&0\\4&1\\5&2\end{vmatrix}$。
这题考察点在计算坐标上，然而只要多开几个变量，就可以完全避免掉计算问题。
可以使用%-3d来向左对齐。
#include <cstdio>
#include <cstring>
int main(int argc, char const *argv[])
{
int a[10][15], b[20][20], c[20][20];
for (int i = 0, cnt = 0; i < 10; ++i)
for (int j = 0; j < 15; ++j)
a[i][j] = ++cnt;
for (int i, j, n, m;
printf("Please input i,j and m,n:"),
scanf("%d%d%d%d",&i,&j,&m,&n), n&&m; )
{
if (i >= 10 || j >= 15)
{
puts("Error! Can not extract submatrix.\n");
continue;
}
memset(b, 0, sizeof b);
memset(c, 0, sizeof c);
for (int x = m-1, ax = i; ax >= 0 && x >= 0; x--, ax--)
for (int y = n-1, ay = j; ay >= 0 && y >= 0; y--, ay--)
b[x][y] = a[ax][ay];
//其实ax、ay坐标是可以算出来的，但是 让电脑算好呢 还是 让人算好呢？
for (int x = 0, cx = m-1; x < m; x++, cx--)
for (int y = 0; y < n; y++)
c[y][cx] = b[x][y];
//其实cx坐标是可以算出来的，但是 让电脑算好呢 还是 让人算好呢？
printf("The submatrix B (%d*%d)is:\n", m, n);
for (int x = 0; x < m; x++, puts(""))
for (int y = 0; y < n; y++)
printf("%-4d ", b[x][y]);
printf("The submatrix C (%d*%d)is:\n", n, m);
for (int x = 0; x < n; x++)
for (int y = 0; y < m; y++)
printf("%-4d%c", c[x][y], " \n"[y == m-1]);
puts("");
}
puts("Programe end.");
return 0;
}
A3、字符串处理（25分）
请按照如下的要求对于字符串中的字符进行消除处理。
（1）每次都从字符串的首元素开始，对连续出现2次（含2次）以上的字符进行处理。
（2）处理的规则为：若连续出现的字符为偶数个，这些连续字符就消除；若连续出现的字符为奇数个，这些连续字符就保留一个。
（3）重复上述消除处理步骤，直到字符串中不再有连续出现的字符为止。
（4）假设原始字符串长度不超过256。
如：原始的字符串为“aaabbaaab”则处理的过程为
“aaabbaaab”→“abbaaab”→“aaaab”→“b”
考察for语句的使用和字符串操作。感觉只能靠代码说清楚了。我在里面加了一些c语言上的技巧。
#include <cstdio>
bool equal(const char *s, const char *t)
{//判断两个字符串是否相等
for (int i = 0; s[i] || t[i]; i++)
if (s[i] != t[i]) return 0;
return 1;
}
bool check(char *s)
{//判断字符串s是否可以继续执行消除操作
for (int i = 0, j; s[i]; i = j)
{
for (j = i; s[j] == s[i]; j++);
//这一步结束以后，s[i~j-1]都是相同的字符
if (j - i >= 2) //j-i就是相同字符的长度
return 1;
}
return 0;
}
void work(char *s)
{
char tmp[256] = "";
for (int i = 0, j, k = 0; s[i]; i = j)
{
for (j = i; s[i] == s[j]; j++);
if (j - i >= 2 && (j - i) & 1 || j - i < 2)
tmp[k++] = s[i];
for (int l = i; l < j; l++) //把s[i~j-1]清空
s[l] = 0;
}
for (int i = 0; tmp[i]; i++)
s[i] = tmp[i];
}
int main(int argc, char const *argv[])
{
for (char str0[256] = "";
printf("Please input the original string, \
enter 'quit' or 'exit' to end this program:"),
scanf("%s",str0),
!equal(str0, "quit") && !equal(str0, "exit");
puts(str0))
for (printf("After processed: "); check(str0); work(str0));
//你真的熟悉for吗hhh
puts("Program end");
return 0;
}
A4、数字处理（15分）
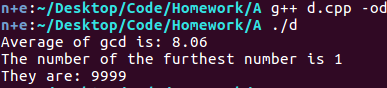
有200个4位正整数，请按照如下的要求编写程序对于这些数字进行处理。
（1）分析每个4位正整数的高三位、低三位分别构成的数值对（假设不考虑低三位数值为000的情况），并计算出每对数的最大公约数；
（2）求所有最大公约数的均值，并找出最大公约数距离该均值最远的所有4位正整数，并将结果输出。
请使用如下的200个正整数：
8478,9782,2622,7840,8933,5163,5057,5820,6929,3882,9808,3508,9704,6034,
5395,7560,7720,8015,6070,7841,7148,5608,2103,4871,9560,1797,7625,4738,
1041,3809,5717,4664,7905,3164,1063,6934,5681,8869,2943,5914,3255,7478,
6722,9625,1611,3063,8920,5996,5245,6640,6783,5192,6145,1377,2216,8342,
4821,3324,5304,4792,1906,1662,8362,5341,3833,5514,2346,7967,8384,5799,
7037,7123,8333,2531,6360,2193,6435,5743,9726,5645,3355,8388,2430,3685,
7188,5270,7860,2667,1246,3553,9999,2133,2043,4970,1435,5803,4799,1951,
5304,9705,3769,5425,3578,4919,1475,5297,4842,2437,8623,5473,2125,7298,
7866,2612,8684,6959,5710,8952,9076,7919,4042,6587,8590,5778,4524,1172,
9130,2827,8826,4059,9679,7734,4973,3532,7638,2205,4784,1960,6808,6469,
9336,5573,6725,8789,5083,2591,2199,2543,5550,3326,6734,5906,2138,1226,
6173,8631,6062,7628,2773,2458,8499,6279,5737,2756,9772,3447,5889,7231,
6084,2633,5578,3985,6605,2835,9270,9612,9334,3765,5545,3621,4189,9912,
3540,5708,5325,6662,5525,5483,6009,5635,6990,5251,6426,5050,2652,8899,
6349,6347,4835,2907
就是一个模拟。我看了好多遍，确定是最远距离。然后看着答案怪怪的。
#include <cstdio>
int gcd(int x, int y)
{
return !y ? x : gcd(y, x % y);
}
#define abs(x) (x>0?x:-(x))
int main(int argc, char const *argv[])
{
int a[200]={
8478,9782,2622,7840,8933,5163,5057,5820,6929,3882,9808,3508,9704,6034,5395,7560,
7720,8015,6070,7841,7148,5608,2103,4871,9560,1797,7625,4738,1041,3809,5717,4664,
7905,3164,1063,6934,5681,8869,2943,5914,3255,7478,6722,9625,1611,3063,8920,5996,
5245,6640,6783,5192,6145,1377,2216,8342,4821,3324,5304,4792,1906,1662,8362,5341,
3833,5514,2346,7967,8384,5799,7037,7123,8333,2531,6360,2193,6435,5743,9726,5645,
3355,8388,2430,3685,7188,5270,7860,2667,1246,3553,9999,2133,2043,4970,1435,5803,
4799,1951,5304,9705,3769,5425,3578,4919,1475,5297,4842,2437,8623,5473,2125,7298,
7866,2612,8684,6959,5710,8952,9076,7919,4042,6587,8590,5778,4524,1172,9130,2827,
8826,4059,9679,7734,4973,3532,7638,2205,4784,1960,6808,6469,9336,5573,6725,8789,
5083,2591,2199,2543,5550,3326,6734,5906,2138,1226,6173,8631,6062,7628,2773,2458,
8499,6279,5737,2756,9772,3447,5889,7231,6084,2633,5578,3985,6605,2835,9270,9612,
9334,3765,5545,3621,4189,9912,3540,5708,5325,6662,5525,5483,6009,5635,6990,5251,
6426,5050,2652,8899,6349,6347,4835,2907}, b[200], sum = 0, cnt = 0;
for (int i = 0; i < 200; sum += b[i++])
b[i] = gcd(a[i] % 1000, a[i] / 10);
float average = sum / 200., max = 0, c[200];
printf("Average of gcd is: %.2f\n",average);
for (int i = 0; i < 200; i++)
if ((c[i] = abs(average - b[i])) > max)
max = c[i];
for (int i = 0; i < 200; i++)
if (c[i] == max)
cnt++;
printf("The number of the furthest number is %d\n",cnt);
printf("They are: ");
for (int i = 0; i < 200; i++)
if (c[i] == max)
{
printf("%d", a[i]);
if (--cnt) putchar(',');
}
puts("");
return 0;
}
清华大学《计算机语言与程序设计》2016年秋季学期 期中测试 （B卷）
B1、字符串处理（25分）
请按照如下的要求对于字符串中的字符进行消除处理。
（1）每次都从字符串的尾元素开始向前处理，对连续出现2次（含2次）以上的字符进行操作。
（2）操作的规则为：若连续出现的字符为奇数个，这些连续字符就消除；若连续出现的字符为偶数个，这些连续字符就保留一个。
（3）重复上述消除处理步骤，直到字符串中不再有连续出现的字符为止。
（4）假设原始字符串长度不超过256。
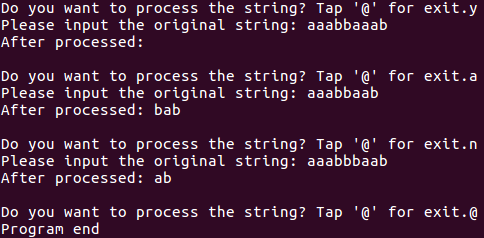
如：原始的字符串为“aaabbaaab”则处理的过程为“aaabbaaab”→“aaabbb”→“aaa”→“”
再如：原始的字符串为“aaabbaab”则处理的过程为“aaabbaab”→“aaabbab”→“aaabab”→“bab”
就是A卷的第三题把一些东西改一下。我为了方便把字符串先翻转，变成从前往后处理，最后再翻回来就好。
#include <cstdio>
void reverse(char*s)
{
int len = 0;
char tmp;
for (; s[len + 1]; len++);
for (int i = 0, j = len; i < j; i++, j--)
tmp = s[i], s[i] = s[j], s[j] = tmp;
}
bool check(char *s)
{//判断字符串s是否可以继续执行消除操作
for (int i = 0, j; s[i]; i = j)
{
for (j = i; s[j] == s[i]; j++);
//这一步结束以后，s[i~j-1]都是相同的字符
if (j - i >= 2) //j-i就是相同字符的长度
return 1;
}
return 0;
}
void work(char *s)
{
char tmp[256] = "", flag = 0;
for (int i = 0, j, k = 0; s[i] && !flag; i = j)
{
for (j = i; s[i] == s[j]; j++);
if (j - i >= 2 && (j - i) % 2 == 0 || j - i < 2)
tmp[k++] = s[i];
if (j - i >= 2)
flag = 1;
for (int l = i; l < j; l++) //把s[i~j-1]清空
s[l] = 0;
if (flag)
for (; s[j]; j++)
tmp[k++] = s[j], s[j] = 0;
}
for (int i = 0; tmp[i]; i++)
s[i] = tmp[i];
}
int main(int argc, char const *argv[])
{
for (char str0[256] = "", read[2];
printf("Do you want to process the string? Tap '@' for exit."),
scanf("%s",read), read[0] != '@';
reverse(str0), puts(str0), puts(""))
for (printf("Please input the original string: "),
scanf("%s",str0), reverse(str0),
printf("After processed: "); check(str0); work(str0));
//你真的熟悉for吗hhh
puts("Program end");
return 0;
}
B2、矩阵处理（30分）
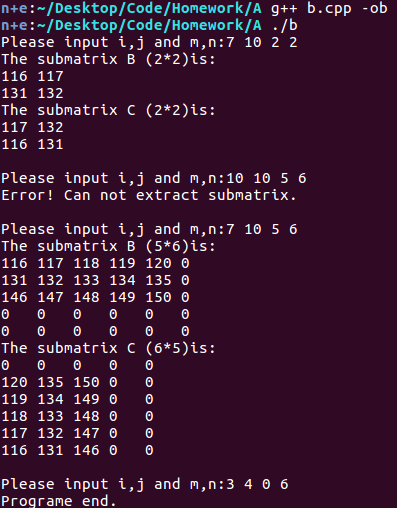
已知一个$M$行$N$列的整数矩阵$A$，请从这个原始矩阵中以$a_{i,j}$为左上角元素抽取一个$m\times n$的子矩阵$B$，要求$a_{i,j}$必须位于$A$中，如果抽取的子矩阵$B$的范围超出原始矩阵$A$的范围，则子矩阵$B$中的这些元素将赋值为$0$。最后请将子矩阵$B$逆时针旋转$90^\circ$，得到结果矩阵$C$。
如：原始矩阵$A$为$\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}$，若输入的左上角元素为$a_{1,1}$，输入的$m$、$n$分别为$2$、$3$，则子矩阵$B$为$\begin{vmatrix}5&6&0\\8&9&0\end{vmatrix}$，旋转后的结果矩阵$C$为$\begin{vmatrix}0&0\\6&9\\5&8\end{vmatrix}$。
A卷第二题。我已经把不同的地方加粗标出来了。
#include <cstdio>
#include <cstring>
int main(int argc, char const *argv[])
{
int a[10][15], b[20][20], c[20][20];
for (int i = 0, cnt = 0; i < 10; ++i)
for (int j = 0; j < 15; ++j)
a[i][j] = ++cnt;
for (int i, j, n, m;
printf("Please input i,j and m,n:"),
scanf("%d%d%d%d",&i,&j,&m,&n), n&&m; )
{
if (i >= 10 || j >= 15)
{
puts("Error! Can not extract submatrix.\n");
continue;
}
memset(b, 0, sizeof b);
memset(c, 0, sizeof c);
for (int x = 0, ax = i; ax < 10 && x < m; x++, ax++)
for (int y = 0, ay = j; ay < 15 && y < n; y++, ay++)
b[x][y] = a[ax][ay];
//其实ax、ay坐标是可以算出来的，但是 让电脑算好呢 还是 让人算好呢？
for (int x = 0; x < m; x++)
for (int y = 0, cy = n-1; y < n; y++, cy--)
c[cy][x] = b[x][y];
//其实cy坐标是可以算出来的，但是 让电脑算好呢 还是 让人算好呢？
printf("The submatrix B (%d*%d)is:\n", m, n);
for (int x = 0; x < m; x++, puts(""))
for (int y = 0; y < n; y++)
printf("%-3d ", b[x][y]);
printf("The submatrix C (%d*%d)is:\n", n, m);
for (int x = 0; x < n; x++)
for (int y = 0; y < m; y++)
printf("%-3d%c", c[x][y], " \n"[y == m-1]);
puts("");
}
puts("Programe end.");
return 0;
}
B3、单词倒序（30分）
假设一个英文语句sentence，该语句中的单词是以空格或逗号为间隔的。请将英文句子sentence中的所有单词进行局部倒序输出。
如，输入的语句为”I love red and sweet apples, you love bananas”，则单词内局部倒序后的语句为”I evol der dna teews selppa, uoy evol sananab”。
再如，输入的语句为” I love red and sweet and big apples, you love bananas.”，则单词内局部倒序后的语句为”I evol der dna teews dna gib selppa, uoy evol .sananab”。(我觉得句逗应该放后面因为它不算单词一部分...)
找分界点，有空格或者逗号就停下。
一个小技巧是在字符串后面加一个空格，处理起来会方便。
#include <cstdio>
void reverse(char *s, int l, int r)
{
for (char tmp; l < r; l++, r--)
tmp = s[l], s[l] = s[r], s[r] = tmp;
}
int main(int argc, char const *argv[])
{
char s[256];
printf("Please input the sentence: ");
gets(s);
for (int i = 0; s[i]; i++)
if (s[i] && !s[i + 1])
{
s[i + 1] = ' ';
break;
}
for (int i = 0, j; s[i]; i = j)
{
for (j = i; s[j] != ' ' && s[j] != ','; j++);
for (reverse(s, i, j - 1); s[j] == ' ' || s[j] == ','; j++);
}
printf("After processed: %s\n",s);
return 0;
}
B4、数字处理（15分）
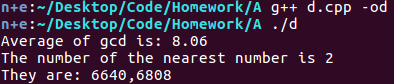
有200个4位正整数，请按照如下的要求编写程序对于这些数字进行处理。
（1）分析每个4位正整数的高三位、低三位分别构成的数值对（假设不考虑低三位数值为000的情况），并计算出每对数的最大公约数；
（2）求所有最大公约数的均值，并找出最大公约数距离该均值最近的所有4位正整数，并将结果输出。
请使用如下的200个正整数：
8478,9782,2622,7840,8933,5163,5057,5820,6929,3882,9808,3508,9704,6034,
5395,7560,7720,8015,6070,7841,7148,5608,2103,4871,9560,1797,7625,4738,
1041,3809,5717,4664,7905,3164,1063,6934,5681,8869,2943,5914,3255,7478,
6722,9625,1611,3063,8920,5996,5245,6640,6783,5192,6145,1377,2216,8342,
4821,3324,5304,4792,1906,1662,8362,5341,3833,5514,2346,7967,8384,5799,
7037,7123,8333,2531,6360,2193,6435,5743,9726,5645,3355,8388,2430,3685,
7188,5270,7860,2667,1246,3553,9999,2133,2043,4970,1435,5803,4799,1951,
5304,9705,3769,5425,3578,4919,1475,5297,4842,2437,8623,5473,2125,7298,
7866,2612,8684,6959,5710,8952,9076,7919,4042,6587,8590,5778,4524,1172,
9130,2827,8826,4059,9679,7734,4973,3532,7638,2205,4784,1960,6808,6469,
9336,5573,6725,8789,5083,2591,2199,2543,5550,3326,6734,5906,2138,1226,
6173,8631,6062,7628,2773,2458,8499,6279,5737,2756,9772,3447,5889,7231,
6084,2633,5578,3985,6605,2835,9270,9612,9334,3765,5545,3621,4189,9912,
3540,5708,5325,6662,5525,5483,6009,5635,6990,5251,6426,5050,2652,8899,
6349,6347,4835,2907
就是一个模拟。我看了好多遍，确定是最近距离。这才科学嘛。
#include <cstdio>
int gcd(int x, int y)
{
return !y ? x : gcd(y, x % y);
}
#define abs(x) (x>0?x:-(x))
int main(int argc, char const *argv[])
{
int a[200]={
8478,9782,2622,7840,8933,5163,5057,5820,6929,3882,9808,3508,9704,6034,5395,7560,
7720,8015,6070,7841,7148,5608,2103,4871,9560,1797,7625,4738,1041,3809,5717,4664,
7905,3164,1063,6934,5681,8869,2943,5914,3255,7478,6722,9625,1611,3063,8920,5996,
5245,6640,6783,5192,6145,1377,2216,8342,4821,3324,5304,4792,1906,1662,8362,5341,
3833,5514,2346,7967,8384,5799,7037,7123,8333,2531,6360,2193,6435,5743,9726,5645,
3355,8388,2430,3685,7188,5270,7860,2667,1246,3553,9999,2133,2043,4970,1435,5803,
4799,1951,5304,9705,3769,5425,3578,4919,1475,5297,4842,2437,8623,5473,2125,7298,
7866,2612,8684,6959,5710,8952,9076,7919,4042,6587,8590,5778,4524,1172,9130,2827,
8826,4059,9679,7734,4973,3532,7638,2205,4784,1960,6808,6469,9336,5573,6725,8789,
5083,2591,2199,2543,5550,3326,6734,5906,2138,1226,6173,8631,6062,7628,2773,2458,
8499,6279,5737,2756,9772,3447,5889,7231,6084,2633,5578,3985,6605,2835,9270,9612,
9334,3765,5545,3621,4189,9912,3540,5708,5325,6662,5525,5483,6009,5635,6990,5251,
6426,5050,2652,8899,6349,6347,4835,2907}, b[200], sum = 0, cnt = 0;
for (int i = 0; i < 200; sum += b[i++])
b[i] = gcd(a[i] % 1000, a[i] / 10);
float average = sum / 200., min = 10000, c[200];
printf("Average of gcd is: %.2f\n",average);
for (int i = 0; i < 200; i++)
if ((c[i] = abs(average - b[i])) < min)
min = c[i];
for (int i = 0; i < 200; i++)
if (c[i] == min)
cnt++;
printf("The number of the nearest number is %d\n",cnt);
printf("They are: ");
for (int i = 0; i < 200; i++)
if (c[i] == min)
{
printf("%d", a[i]);
if (--cnt) putchar(',');
}
puts("");
return 0;
}
2017年1月02日 16:33
金牌爷竟然担心大学程序设计
2017年1月05日 22:51
@NoNoSS: 并没有啊。。。我只是给同学写一下，有些人是零基础