在这个页面某个角落有张小纸条，大家可以找找看~

微积分

听说作业很难？

现在发答案不太好。我卡的比较久的是第一题，花了20min……

这里提供一个idea：为什么题目里有 $\frac{1}{n}$ 而不是 $\forall \alpha\in [0,1]$？于是就能把这个区间分成 $n$ 段来考虑。剩下的就没什么了吧……

素拓：n次多项式有n个根

这件事情就是陈酌老师上课讲的，传说中的代数基本定理，现在我们要用一种炫酷的方法证明它。唯一所要知道的就是复数的几何意义和 $e^{i\theta}=\cos\theta+i\sin\theta$

首先要知道，证明 $n$ 次多项式有 $n$ 个根，只要证明有一个根就行了，然后把这个根通过因式分解分出来，剩下 $n−1$ 次多项式，重复这个过程就可以找到 $n$ 个根。

设多项式为 $$f(z)=a_0+a_1z+a_2z^2+\cdots+a_nz^n$$ $z$ 和 $f(z)$ 都可以是复数，$f(z)=0$ 就是要让$\mathrm{Re} f(z)=0$ 且 $\mathrm{Im} f(z)=0$。

当 $|z|$ 很大时，忽略低阶项，$f(z)=a_nz^n$。设 $z=re^{iθ}$，那么 $f(z)=a_nr^ne^{in\theta}$，$\mathrm{Re}f(z)=0$ 就是要让 $n\theta =(k+\frac{1}{2})\pi$，$\theta = (\frac{k}{n}+\frac{1}{2n})\pi$。

$\theta\in [0,2\pi)$，那么 $\mathrm{Re}f(z)=0$ 对应的就是 $2n$ 条射线，同理 $\mathrm{Im}f(z)=0$ 对应的是另外 $2n$ 条射线，$n=3$ 且 $|z|$ 很大时如图。

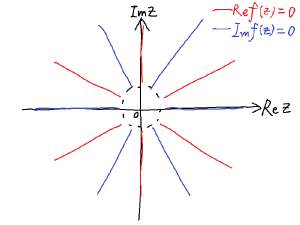
其中红线为 $\mathrm{Re}f(z)=0$ 的图像，蓝线为 $\mathrm{Im}f(z)=0$ 的图像，黑圈里表示 $|z|$ 不太大时的情况，现在还不知道，一种可能的情况如图，红线和蓝线的交点就是 $f(z)=0$ 的根。

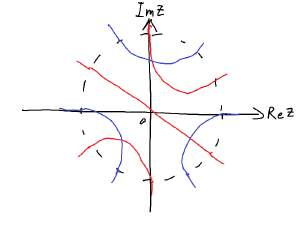
但是 $f(z)$ 是一个光滑的函数，那么圈里的红线应该把圈外的红线两个一组相连，而且不会出现三条线交叉在同一点的情况，否则就不光滑了。如果四条线交叉在同一点，我们可以把交叉点分开，当作它们没有相交。蓝线也是这样。

于是“$n$次多项式有$n$个根”这个问题被我们转化为了一道炫酷的奥数题：圆周上相间排列着 $2n$ 个红点和 $2n$ 个蓝点，用不相交的红线把红点两个一组相连，不相交的蓝线把蓝点两个一组相连，求证红线和蓝线一定相交。用奇偶性很容易证明。

当然没有哪本高数书会讲这么炫酷的方法，$idea$ 来自克莱因的《高观点下的初等数学》。

线性代数

听说大家上课都不听了？

那我也没办法咯……我坐在后排还听到有人说听这些课侮辱智商……感觉药丸

叉积的性质

拉格朗日恒等式$$|\bf{a}\times \bf{b}|^2=|\bf{a}|^2|\bf{b}|^2-(\bf{a}\cdot\bf{b})^2=\begin{vmatrix}\bf a\cdot \bf a&\bf a\cdot \bf b\\\bf b\cdot \bf a&\bf b\cdot\bf b\end{vmatrix}$$

雅可比恒等式$$\bf a\times (\bf b\times \bf c)+\bf b\times(\bf c\times \bf a)+\bf c\times (\bf a\times \bf b)=\bf 0$$

拉格朗日公式$$\bf a\times (\bf b\times \bf c)=\bf b(\bf a\cdot \bf c)-c(\bf a\cdot \bf b)$$

程设

普及小Trick

李宛洲这周考试并且没作业，看了一下刘连成的作业。有一些还是有必要讲的。

1.三角形的面积和周长

多组数据循环应该这样写：

scanf("%d",&repeat);
for(int i=1;i<=repeat;i++)
{
	...
}

其实正常来说没有repeat这样给变量起名的，一般都是T或者TestCase

2.竖式打印

你真的了解printf的格式串的用法吗？

printf("%4d",a); 表示如果a的长度小于4位的话，那么就在a前面补上空格直至4位为止，不信可以拿vs试试 printf("%5d\n",233);

所以根本不需要写什么if(a>1000)...;else if(a>100)...;else ...之类的东西，我大概写了一下长成这样：

#include<cstdio>
int a,b;
int main(){
	scanf("%d%d",&a,&b);
	printf("%5d\n*%4d\n------\n%5d\n%4d\n------\n%5d\n",
a,b,a*(b%10),a*(b/10),a*b);
}

3.铅笔工厂

gcd(a,b)表示a,b的最大公约数，高中课本告诉我们：gcd(a,b)=gcd(a-b,b) (假设a>b)，再变个型就是 gcd(a,b)=gcd(b,a%b)。

于是只要写个函数

int gcd(int x,int y){return!y?x:gcd(y,x%y);}

然后直接调用gcd(a,b)就能得到a和b的最大公约数了。这样子只要调用 $O(\log(\max\{x,y\}))$ 次就能解决

什么你看不懂？

(!y) 等价于 y==0

表达式A?表达式B:表达式C 等价于 if(表达式A) 表达式B; else 表达式C; ?:也称作三目运算符

注意不能在表达式里面加‘;’，如果要一次性执行很多条语句的话，这样子：a==0?(x=b,y=c):(x=c,y=b);

函数是啥？在这里映射名称叫做gcd，自变量为x和y，到达域为R，然后把算出来的答案返回掉，gcd(x,y)才能有值。

Q: 为啥要这样写？我一个个判断不是也可以吗？

A: 通常情况下，计算机一秒大约能够处理一亿条语句（表达式），比如i++、a+b这样的东西。数据一大，跑的就很慢了。然而log的效率是远远要优于线性的。而且你不觉得这样写比你枚举还要短吗？

6.极限求值

这玩意儿就是在求 $\sin 1$ 的值。【逃

7.数列求和

你真的了解for吗？

#include<cstdio>
int n,a,s,x;
int main(){
	for(scanf("%d%d",&n,&a);n--;s+=x)x=x*10+a;
	printf("%d\n",s);
}

8.素数求和

当然可以一个个数判断，不过太暴力了。

男生们要想在妹子面前show一发，就需要提高自己的姿势水平。

大规模求素数的方法（指求1~n中的所有）有欧拉筛（效率$O(n\log n)$）、线性筛（效率$O(n)$）；小规模求素数（指只求一个）的方法有Rabin-Miller。有兴趣的同学可以戳这里

欧拉筛很容易懂，就是枚举i，把i的倍数标记为不是素数。这样总共要做 $\frac{n}{1}+\frac{n}{2}+\cdots+\frac{n}{n}\sim n\log n$ 次，当n=1000000也没问题，能在1s内出解。

#include<cstdio>
int m,n,sum,vis[510]={1,1};//0表示是质数，1表示不是质数
int main(){
	scanf("%d%d",&m,&n);
	for(int i=2;i*i<=n;i++)if(!vis[i])
	for(int j=i+i;j<=n;j+=i)vis[j]=1;
	for(;m<=n;m++)if(!vis[m])sum+=m;
	printf("%d\n",sum);
}

11.方程求根

啥是牛顿迭代法呢？就是先随便给个点$x_0$，在 $(x_0,f(x_0))$ 处作切线 $l_0$，交$x$坐标轴于点 $x_1$，这样一直做会有 $x_2,x_3,\cdots,x_n$出现，并且收敛于某个零点。

具体要怎么求呢？根据刚才的定义手推公式就好了：$$x_{n+1}=x_n-\frac{f(x_n)}{f^\prime(x_n)}$$

思修

作业11答案

D;C;B;D;ABD;