圆的反演
题目大概是这样的:
有很多圆,满足 $C_n(n\ge 4)$ 与 $C_1,C_2,\cdots ,C_{n-1}$ 都相切,$C_3$ 与 $C_1,C_2$ 相切,$C_2$ 与 $C_1$ 相切,图形如下:
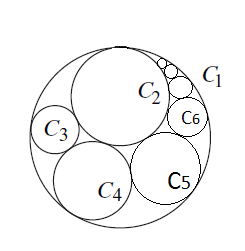
现已知 $r_1,r_2,r_3,r_4$,求 $r_n$。询问数<=1000w,$n\le 10^9$,时限 $1.5s$
例如:当 $r_1=6,r_2=r_3=3,r_4=2$ 的时候,圆大概长这样:
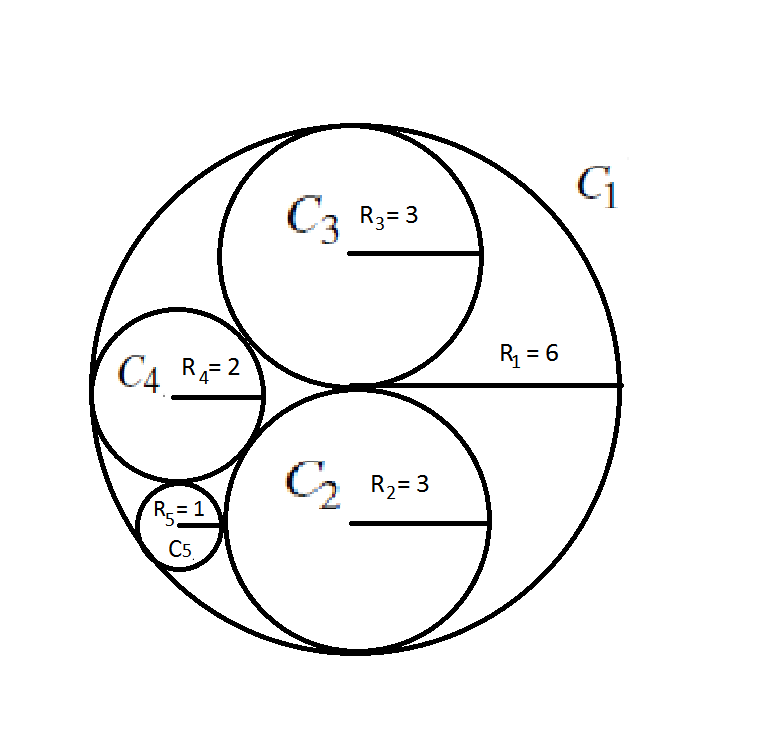
圆的反演是什么呢?
我们先选定一个点 $O$为反演中心,以 $O$ 为圆心,半径为 $r$ 画一个圆。然后对于平面上的点 $P$ 和 $P'$,如果 $P$ 和 $P'$ 在以 $O$ 为起点的射线上,并且 $|OP|\cdot|OP'|=r^2$,那么就说 $P$ 和 $P'$ 互为反演点。
所以圆外的点反演一下会到圆内,圆内会到圆外,圆上则不变。
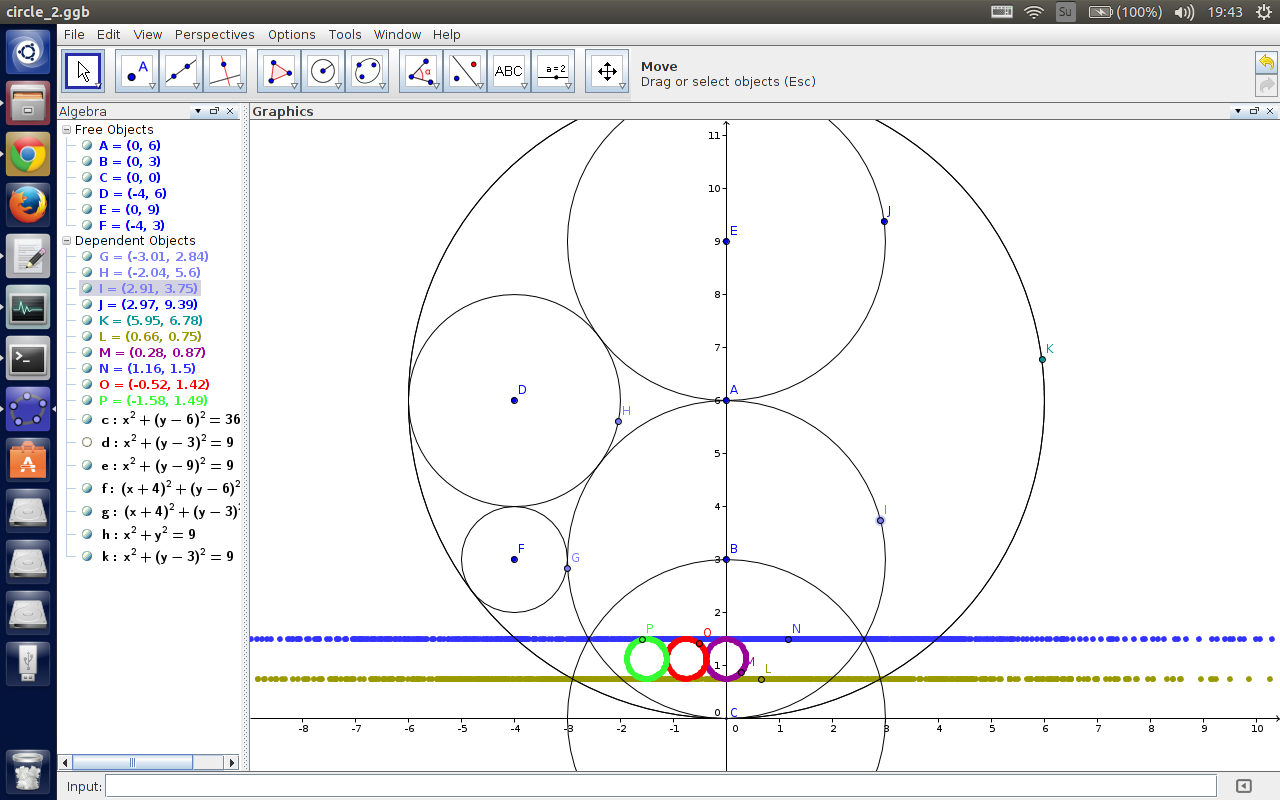
我找了 $GeoGebra$ 来玩玩,效果差不多是长下面这个样子的:
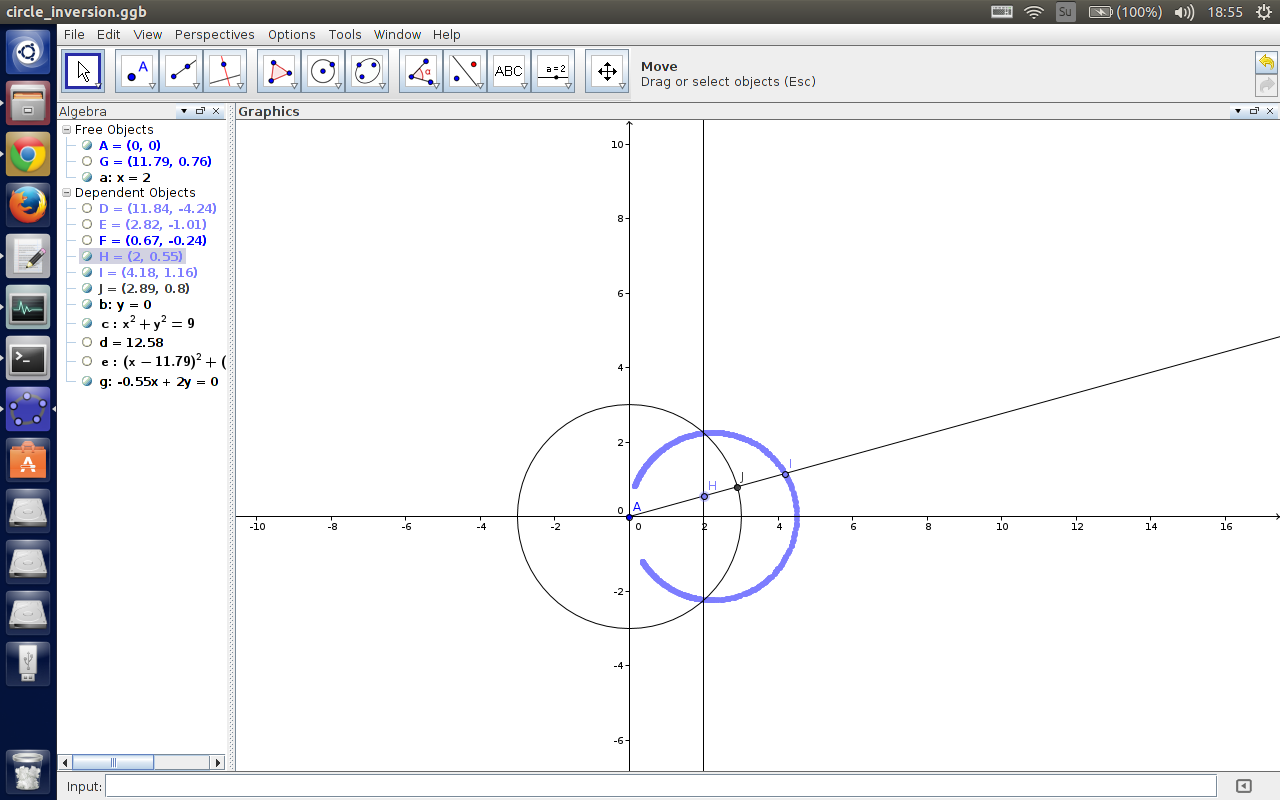
反演中心为坐标原点,点 $H$ 在直线上移动,点 $J$ 为射线 $AH$的焦点,点 $I$ 为点 $H$ 的反演点。
(图片是可以点开来看的...)
可以看到,一条不过反演中心的直线反演之后变成了一个过反演中心的圆。而且直线和两个圆两两相交。
由于反演的可逆性,这个圆反演一下就变成了一条直线啦~
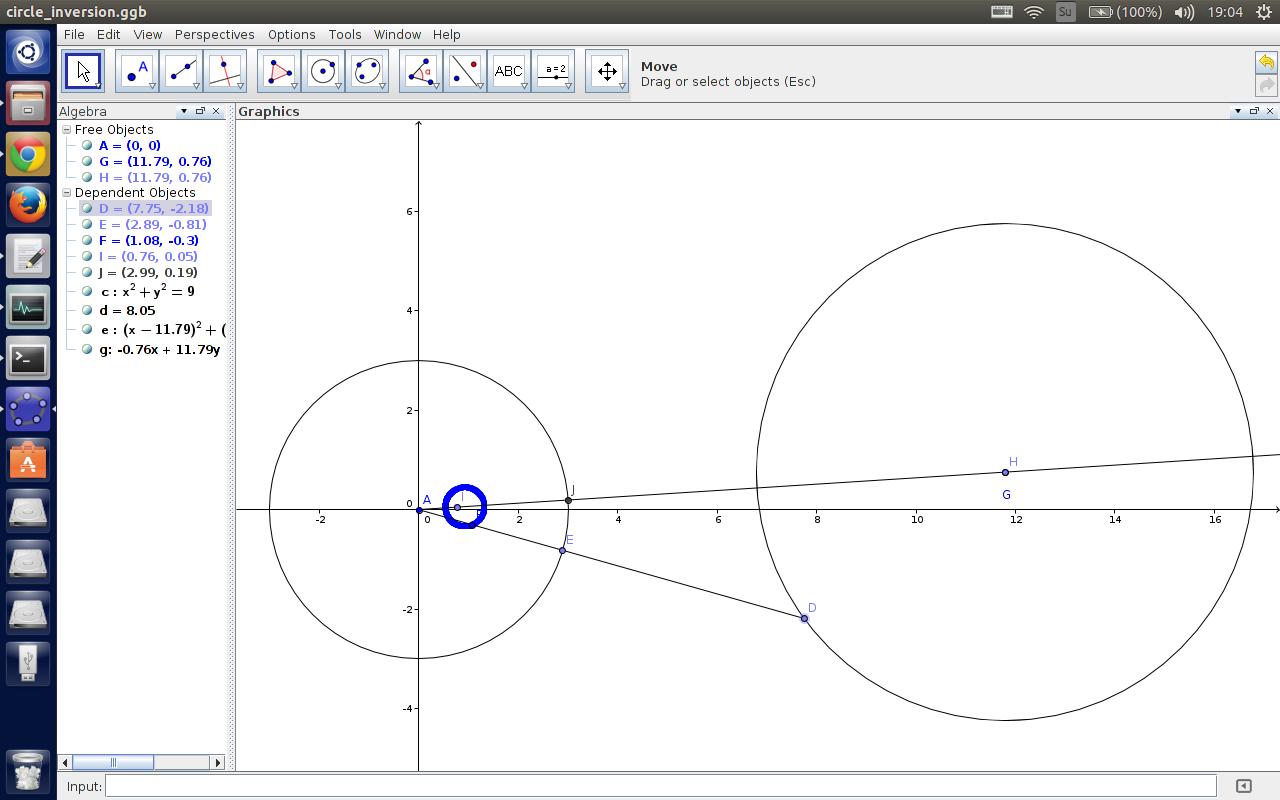
一个不过反演中心的圆反演以后是一个以反演中心位似的圆。
从上面的图来看,显然两个圆是反过来对应的,并不是直接位似。还有切记,圆心反演完以后并不是反演完的圆的圆心,比如上面的点 $H$ 和 $I$。
再来一个好玩点的:
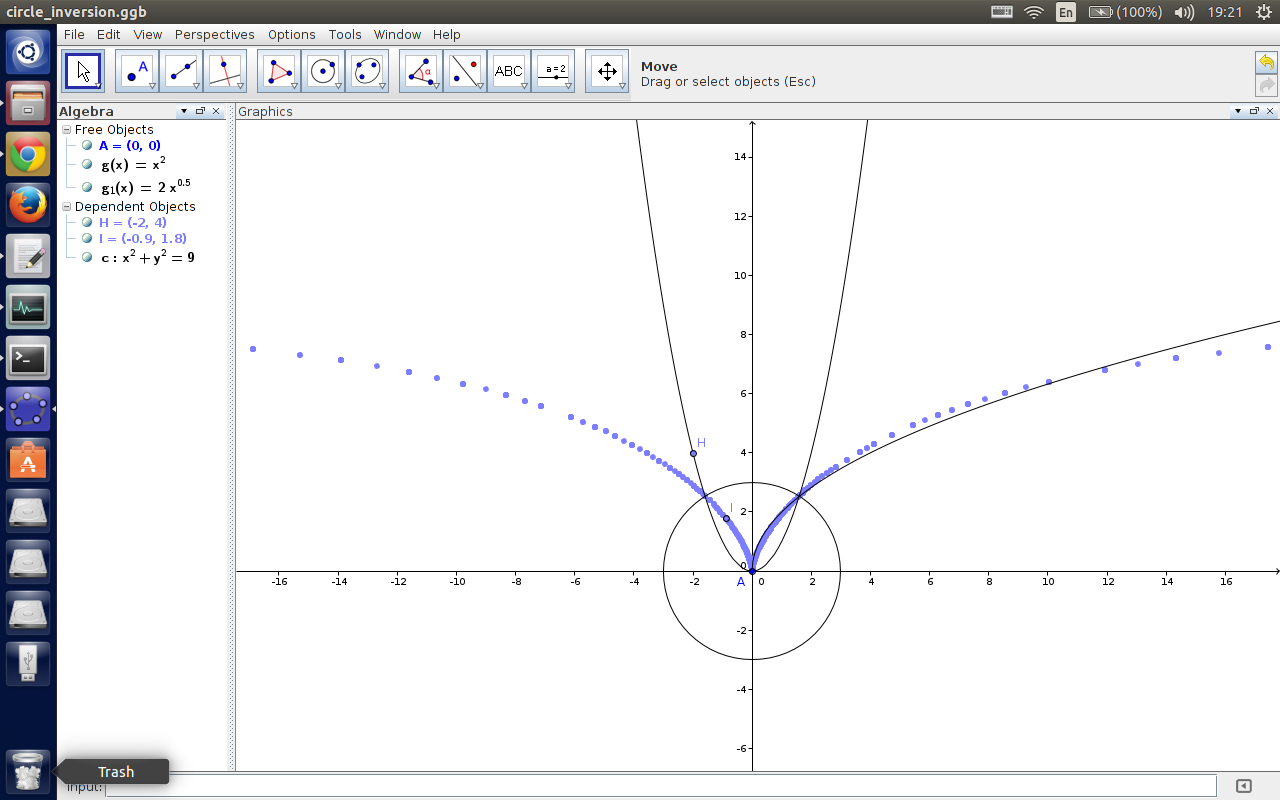
抛物线反演一下,不知道变成了什么。。。右边的黑线是 $2\sqrt{x}$,然而不能拟合。
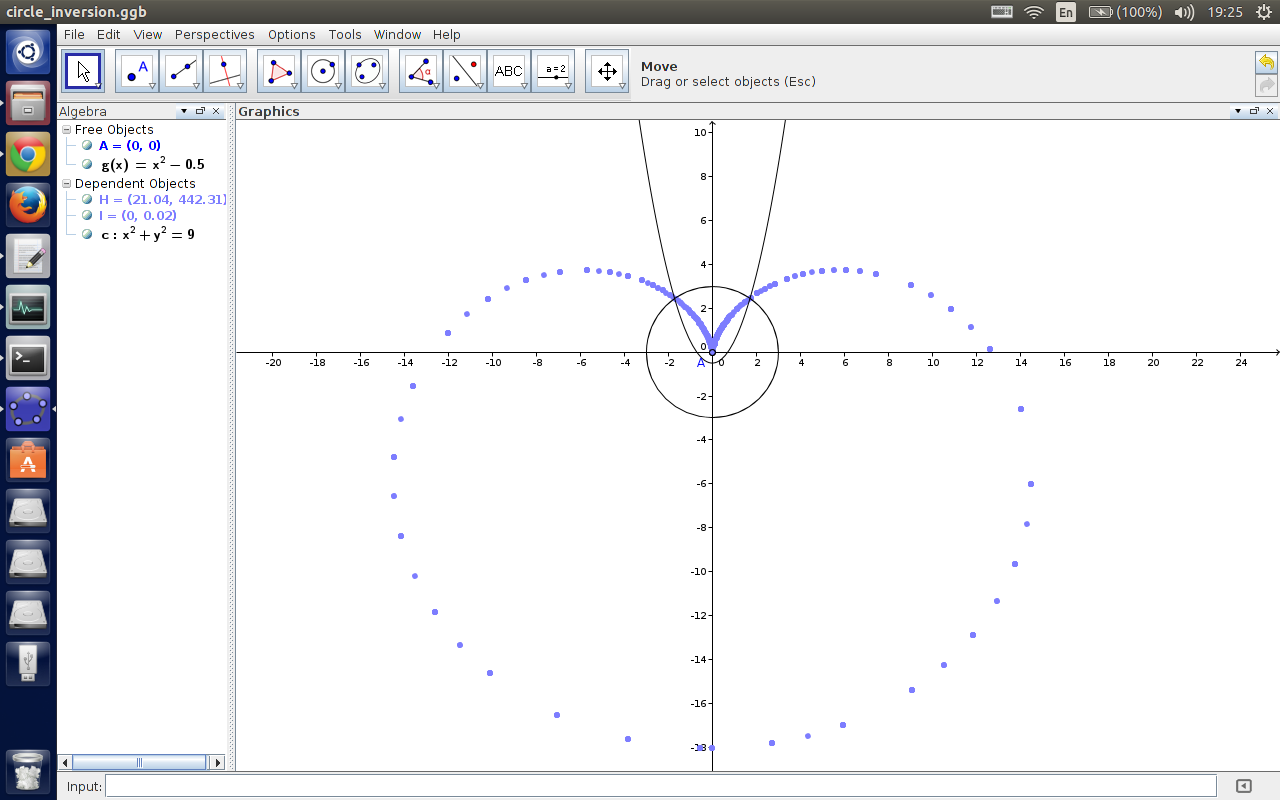
然后稍微往下移一点就变成了心型线!
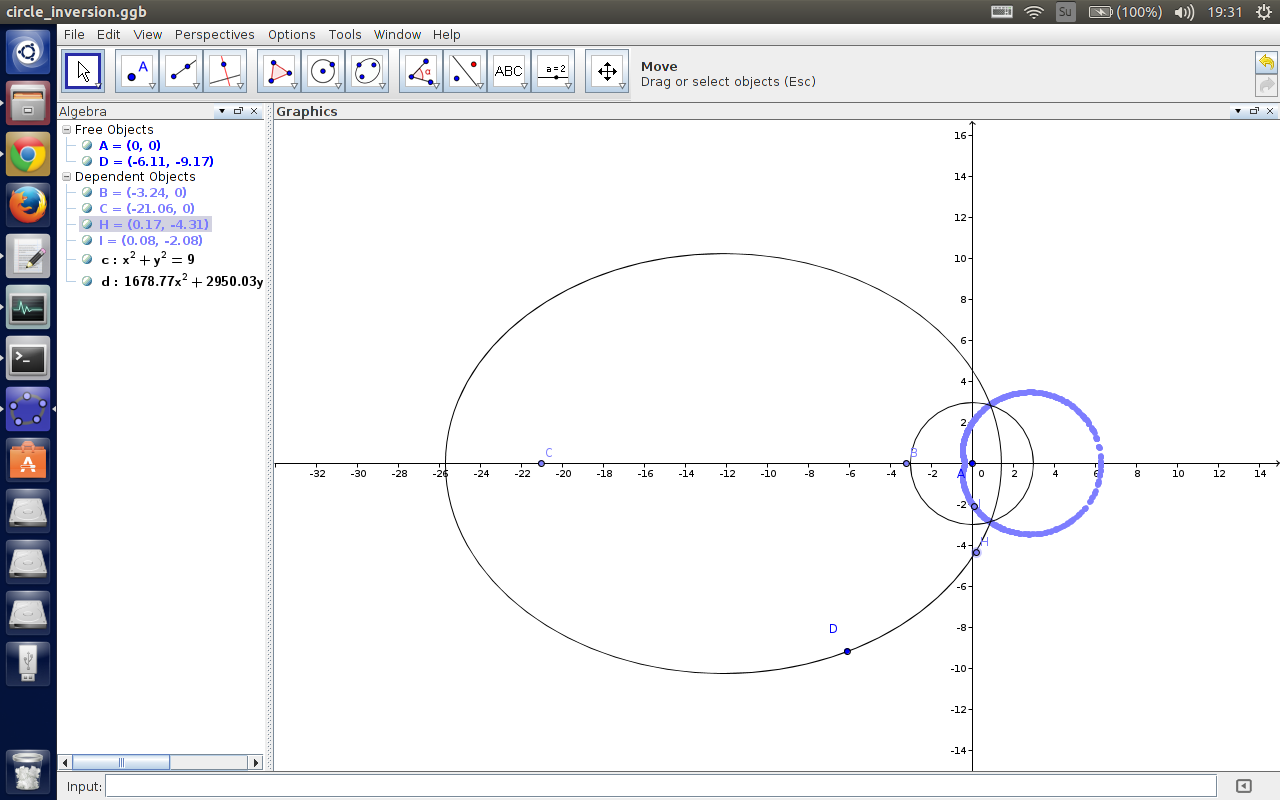
椭圆好像跟上面两种差不多,不是太好玩。
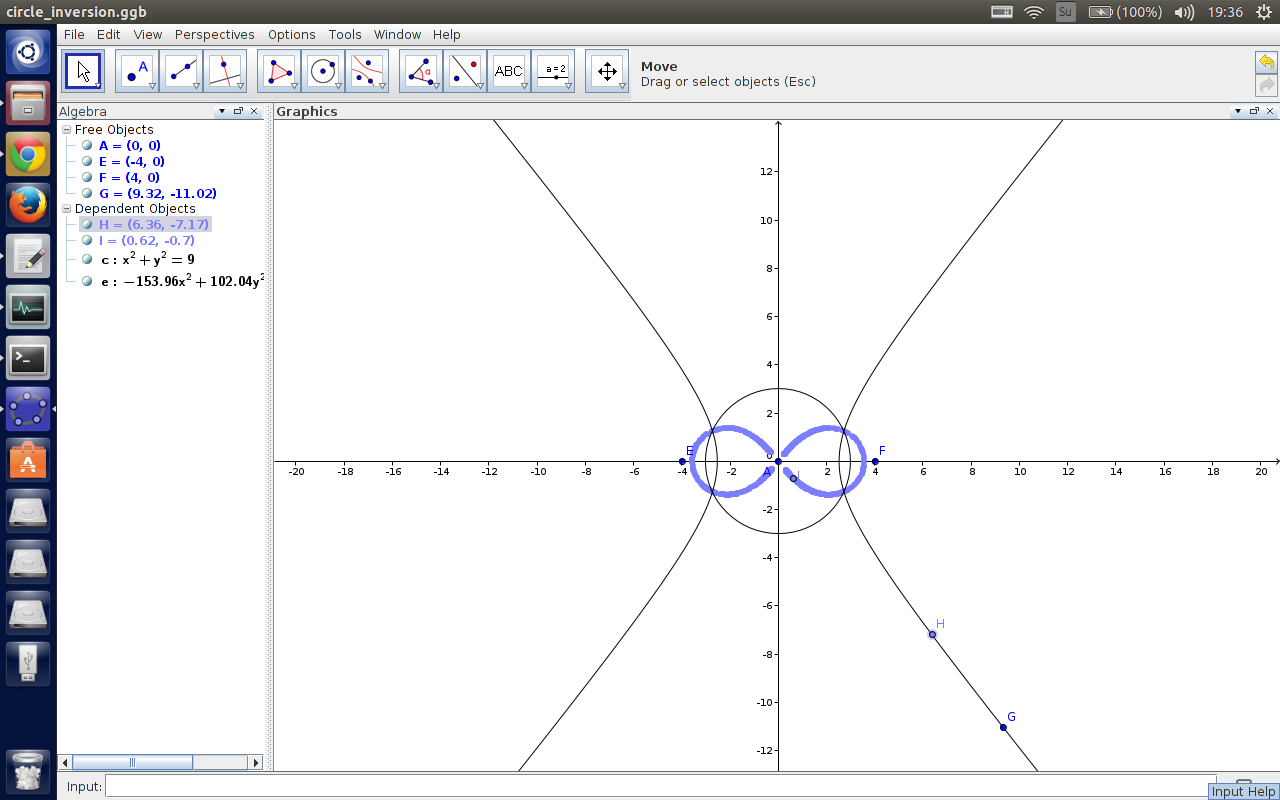
双曲线反演一下变成了 $\infty$...
我们不妨把样例反演一下变成下面这样:
由于反演前后的几何性质是不会发生改变的,比如反演前两个圆相切,反演完以后他们两个还是相切,只不过可能不是圆与圆相切而是直线与圆相切之类的,因此我们可以像这张图这样建立反演中心,圆 $C_1,C_2$ 反演完以后就变成了两条直线,而 $C_3,C_4,\cdots$ 反演完之后,由于没过反演中心,所以还是圆;又因为它们都与圆 $C_1,C_2$ 相切,所以反演以后的圆统统都被夹在了两条直线里面,大小都一样,而且一个挨着一个。
然而我觉得如果不会求的话,可以随便找圆上的三个点,然后把这三个点反一下,然后再以这三个点画个圆就好了,简单粗暴= =
注意不能直接求圆心。原因在上面第二张截屏。
于是这题的解法已经十分明了了:先把 $C_1,C_2$ 反成直线,解三角形解出 $C_3$ 的位置,然后反成小圆,看一下 $C_4$ 塞哪里符合题意,然后就可以 $O(1)$ 求出第 $n$ 个圆反演完以后的圆,直接反回去就好了。
#include<cstdio>
#include<cmath>
typedef double ld;
struct P{
ld x,y;
P operator*(ld a)const{return(P){x*a,y*a};}
P operator/(ld a)const{return(P){x/a,y/a};}
}o3;
ld len2(const P&a){return a.x*a.x+a.y*a.y;}
P xorr(const P&a){return a/len2(a);}
int n,p,m,b,t;ld r,A,B,C,cosB,sinB,st,ans;
struct Cir{P o;ld r;}c[5],d[5];
Cir xorr(Cir a){
ld d=sqrt(len2(a.o)),r=(1/(d-a.r)-1/(d+a.r))/2;
a.o=a.o*(1/(d-a.r)-r)/d,a.r=r;
return a;
}
int main(){
scanf("%d%d%d%d%d",&t,&n,&p,&m,&b);
scanf("%lf%lf%lf%lf",&c[1].r,&c[2].r,&c[3].r,&st);
c[1].o.y=c[1].r;c[2].o.y=c[2].r;
d[4].r=r=(xorr((P){c[2].r,c[2].r}).y-xorr((P){c[1].r,c[1].r}).y)*.5;
A=c[1].r-c[2].r,B=c[2].r+c[3].r,C=c[1].r-c[3].r;
cosB=(A*A+C*C-B*B)/2/A/C;sinB=sqrt(1-cosB*cosB);
c[3].o.x=C*sinB;c[3].o.y=c[1].r-C*cosB;d[3]=xorr(c[3]);
d[4].o=(P){d[3].o.x+r+r,d[3].o.y},c[4]=xorr(d[4]);
if(std::abs(st-c[4].r)>1e-9)r=-r;
for(r*=2;t--;){
n=1LL*p*n%m+b;
if(n<=4)ans+=c[n].r;else{
d[4].o=(P){d[3].o.x+r*(n-3),d[3].o.y};
register ld _d=sqrt(len2(d[4].o)),_r=(1/(_d-d[4].r)-1/(_d+d[4].r))/2;ans+=_r;
}
}
printf("%lf\n",ans);
}
2017年8月11日 13:08
请问聚聚有这道题的地址吗,
2017年9月11日 21:55
@zzzz: CC2015 NTHCIR
2019年9月15日 20:05
High quality services for the trained and additionally experienced worker bestowed them for the best housecleaning company for Dubai. You should agree that every type about cleaning service differs from its own matters. Therefore, the service plan demands a trained person in each one of the fields needing sufficient experience on the relevant line of business of service plan.
2019年11月14日 01:08
or a lot of us, buying home is the foremost costly not to mention significant money they'll ever previously make throughout their lives. Therefore, it helps to be in the recognize how to spend a mortgage profit wisely.
2020年3月20日 18:06
Online business list happen to be compiled together with updated once a month with help of numerous sources which include yellow sites directories, business credit card, annual information, business together with industry internet sites, and phone number verification.
2020年3月20日 18:06
Online world Buisness, web marketing and posting all choose together good. In selected, you will add copy links towards your blog articles or blog posts. These one way links will fire your internet page viewer through to your web site for an individual's affiliate process.
2020年3月20日 18:07
For those who hate getting out of bed each and every morning and attending work for some other individual, then critiques an internet home business. People make it happen for many reasons, like being when using the kids or simply just a improve of standard of living.
2020年3月20日 18:08
Online Marketing may be a broad term this includes advertising, advertising and marketing, and strengthening the webs presence for businesses thru digital podiums. Some within the digital maneuvers that fit in the coverage of 'Digital Marketing' happen to be digital advertisements, email internet marketing, content internet marketing, pay-per-click, on line brochures, even more.
2020年3月20日 18:09
Common and Significant Health Projects - The quality of a limited insurance coverage benefit on a considerably decreased insurance value. In choosing this health protection plan, it is recommened that you are required to read any policy brief description giving special look into covered products. There happen to be plans which will not take care of on certain basic treatment plans, certain health related services which include chemotherapy, maternity care or simply certain prescription medications.
2020年4月28日 20:07
As you hire an important servant maid to freshen up you office or house, you can be permitting her access to to your current belongings. As a result before hiring people a house maid, you should really ask positive questions to discover more about her record information and even personal qualifications. First item is which will, you should really inquire buddies, relatives and acquaintances with regard to personal experience considering the servant service personnel.
2021年6月07日 13:54
Together with, this comprises kitchen floors and walls and under the dining desks. Moreover, weekly or simply daily cleaning is very in line with the amount for dirt or simply grime having accumulated inside the house. However, you need to opt meant for curtain cleaning to build your place germ-free.